本文刊发在《程序员》杂志09年第二期上。是讨论函数式语言基本性质和发展方向的一篇文章。
一、把大象装进冰箱
在命令式语言（当然我们可以确指为C、Delphi、Java或C#等等）中，初学者的第一个疑难便是这样的代码（注1）：
X=X+1
为什么？因为在数学概念中，上述等式是不能成立的。这种表达式是计算机的思维逻辑：当它运算上述表达式（或语句）时，X被作为暂存单元——例如冰箱。为了让冰箱产生变化，比如解决“把大象装进冰箱”这样的问题，我们需要如下三步：
把冰箱门打开，把大象放进去，把冰箱门关上!
（图1：“把大象装进冰箱”的问题）
因为我们有两只手来分别负责拉住冰箱门和大象，所以整个操作过程看起来很完美，但接下来我们再加上点需求：我们要“把大象拿出来，把长颈鹿装进去”，怎么办？是的，应该这样：
把冰箱门打开，把大象拿出来，把长颈鹿装进去，把冰箱门关上。
可惜长颈鹿有腿有思想，所以问题将会出在我们把大象拿出来的那一时刻：长颈鹿跑掉了。为此，我们必须做很多的防护措施，例如先锁住长颈鹿，再锁住大象，以及在整个过程中，保证冰箱门不会自动关上或打开……而代码：
X=X+1
的执行过程与此类似：当CPU开始存取X这个位置时，它只能在“当前X”与“下一次X”之间选择二者之一。当多个线程（或多个CPU）开始存取X这个位置时，如果我们希望得到相同的X值，那么我们就得在X操作过程中采取象上面一样的防护措施：加一个锁。以保证要求所有线程都取完了这个“当前X”值，才会被切换到“下一次X”值。
由于这个限制，一旦多个线程都排着队来看看这个X的美妙身形，整个队列就全都慢下来了。
解决这个问题的办法其实很简单：只要X可见，我们就永远不修改这个X。而这，就是函数式应对大象问题的方法：如果冰箱里放着大象，就永远不要试图放长颈鹿。所以在函数式语言Erlang中的变量一旦赋值，就不能再修改。
云风曾在SD2C 2007大会上说：解决问题的最好方法，就是不解决它。这个观点深得函数式的精髓。
二、帽子戏法的关键，在于至少多一顶帽子
杂技中的一种常见帽子戏法，是很多人围成一圈或排成一排然后飞速地传送手中的帽子。这如果是一个人来表演，那么应该是左右手各一顶帽子，而多出的一顶则总在头上。
（图2：帽子戏法）
所以，关键在于至少要多出一顶帽子。正因为多出来这个帽子，所以我们看到杂技师在我们面前构建了一个往复不休的循环。事实上程序设计里的“循环”也存在完全相同的问题：我们至少需要一个变量来保存迭代中的计数，而且这个变量必须是可以修改的(注2)。然而这一要求既是玩转“帽子戏法”的必要条件，却又与我们上面讲过的“不修改变量”的原则相违背。
函数式如何解决这个问题呢？
其实答案还是相同的答案：至少多一顶帽子。只不过，帽子不一定要放在头上，我们可以把它放在传递的过程中——例如空中——就可以了。要知道，让杂技师用同样的方法来掷苹果，那多出来的一个就总是在空中了。
在函数式中，我们如果要构建一个循环，那么可以使用函数递归来实现。这上述控制循环过程的变量，则可以把它放在函数形式参数表——这种类似“空中”的地方。与“空中”相同的是，我们在静态看函数时，那是参数表；而运行中时，它传入实参。
然而帽子戏法的表演者并没有三只手或更多只手，被循环帽子增加的时候，杂技师除了加快速度之外，保证一个简单的原则也是极其重要的：总是从帽子队列的最末端取到下一只帽子。这一原则保证了可以容纳更多帽子，而又不会少处理任何一个。同样的，递归是消耗栈的，为了使栈空间不爆炸，解决的方法就是在最后一行代码上调用递归，即尾递归。因为尾递归的存在，函数最末的调用就可以被优先为一行不消耗栈的跳转指令，就像帽子戏法的杂技师从帽子队列上直接取走轮转到手边的帽子一样。
最后，对于一个函数来说，如果它只返回值而不修改函数外的任何东西，那么这个函数就是安全的，它等价于它返回的这个值——如前所述的，这个值一旦有效（运算出结果并传出），就不再变更。所以函数式中的函数调用，可以等价于一个表达式中运算的值。
如同函数调用，函数的递归也只返回值，所以也等价于一个表达式中运算的值。再进一步的推论，递归实际上等效于循环求值。
复杂的表象下，总会有一个简单的原则。万人的与一个人的帽子戏法，其原则是一样地：至少多一顶帽子，放在头上，或是空中。
三、计算机其实不认得"hello"
32位的unicode，以及128位的GUID等等，都直接与我们现在或将来的存储单位以及运算的通道大小有关。事实上即使我们有128位机器，我们也只打算在这样的通路上传送一个字符"h"——而不是字符串"hello"。从更为准确的角度来说，事实上计算机也不认得字符"h"，而只认得数字0x68。同样的，它也不认得所谓的“真假(true/false)”，而只认得数字的1/0。
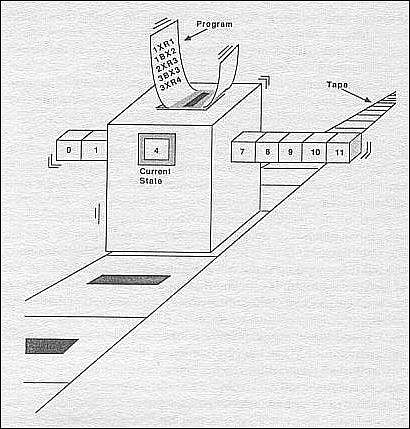（图3：图灵机的概念图）
我们编程的本质，其实不过是在求值一些数字而已。只是最终我们在自然语义上把这些数字的一个连续或非连续的集合认为是布尔值、字符串、数组或对象。当我们认识到运算求值的结果无非是数值，而表达形式又无非是连续或非连续时，我们就得到了基本的数据抽象单元：值、值系列。再加上我们前面讲到的执行体（函数），我们就得到了整个函数式语言的鼻祖——LISP——的基本运算模型：
(+ Xn)
其中，“( )”表明一个值系列（表），而“+”在这里指代某种运算，Xn表明值（或值系列）。整个的表返回一个值，因此也可以将“整个的表（通常这里称为表达式）”等义为一个值。任何的一个运算，最终输出的仍然只是一个或一系列数字，它被显示在屏幕上，便成了文本；放在内存中，便成了数据。
当然，现实是这样的机器最终从科学领域走向了民用，在PC（个人计算机）普及的现在，我们也需要让类似LISP这样的——绝对正确而又绝对非人性的——语言变得亲切一些。于是稍微复杂而有用一点的函数式语言，例如Erlang，通过丰富了上述的基本运算模型来使我们的视觉愉悦，或是在讨论它的代码时显得神经（略为）正常一些：
类型 示例 值 atom,integer/float,... 值系列 list(不定长的表，一般非连续存储) tuple(定长的，一般连续存储) 运算 函数。特定函数包括：if..end，case..end等。
（表一：以Erlang为例的、简单的类型抽象）
而我们逆推一份具体的Erlang代码，其实仍然可以表达为上述的(+ Xn)。例如我们可以在Erlang代码在编译阶段使用解析树（Abstract Form）中看到这样的抽象代码（abstract code）：
[{abstract_code,
{raw_abstract_v1, [{attribute,1,file,{"./simplest.erl",1}}, {attribute,1,module,simplest}, {function,3,test,0,
[{clause,3,[],[],[{atom,4|...}]}]
},
{eof,1}]
}
}]
无论是从形式，还是从实质来看，这种解析树（在erlang执行中将会按照解析树来生成语法树并执行）与LISP语言的基本原则都是一致的。
四、从“函数等义于值”到“函数是值”
现在，JavaScript语言被更为深入的挖掘并渐渐了解到它的函数式语言本质，而类似Erlang这样的“天生伤害人的视力”的语言也移步前台。这些语言的努力，使我们终于看到一个属于函数式语言的时代的曙光。在黎明之前的黑暗中，函数式以它诸多的、最不可思议的特性迷惘着程序员的目光。连它最基本的概念说明，也如同玄学家的呓语：如同数学函数是集合A（称为定义域）中成员到集合B（称为值域）中成员的映射，函数式语言就是通过数学函数的定义、应用的说明和求值完成运算过程的。
类似于这种等同于“什么也没说”的解释，其实的确是在阐述函数式语言的精髓。为了减轻你的痛苦（但绝非轻视你的智商），我通常换个说法来陈述它们：如果表达式“1+1=2”中的“+”被理解为求值函数，那么所谓函数式语言，就是通过连续表达式运算求值的语言；既然上面的表达式可以算出结果“=2”，那么函数式语言自然也可以通过不停地求值找到问题的答案。
首先，在函数式语言中，函数只表明一个运算过程，并产生一个运算结果。这与表达式中的运算符具有完全相同的性质——所以事实上一个函数式语言中，表达式的运算符被实现为一个函数。例如erlang的核心模块中，可以导出类似这样的函数：
函数名/参数个数 函数名/参数个数 函数名/参数个数 '!'/2 '+'/1 '-'/1 '*'/2 '+'/2 '-'/2 '++'/2 '--'/2
（表二：Erlang中的运算符其实对应于内核函数－部分举例）
所以，函数式语言的本质是表达式/函数的“连续求值”。既然我们的输出或存储最终只是在关心“值”，那么显然连续求值的结果就可以直接作为他们的输入。如果把输出终端或存储看成接受输入的设备，那么他也相当于一个函数；如果一台计算设备只对外界表达为一个或一系列输出，并接受来自其他类似设备的输入，那么计算设备本身也可以视为一个函数……
我们将这个过程放大，其实网络可以是函数式的。这个就是著名的语用网，它的理论基础是petri网论（Petri nets theory）。而事实上，作为计算模型来理解，它与函数式语言是相似、等价的（注3）。
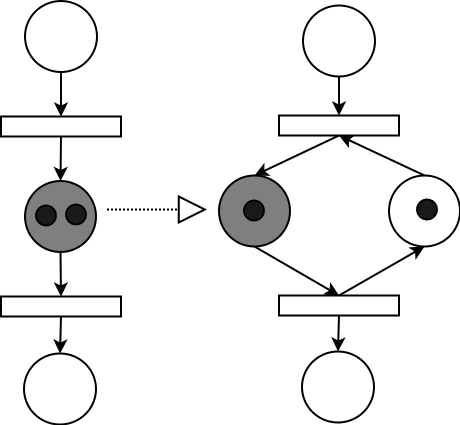图4：perti网的“库所变换”
函数式语言通过函数实现了三个基本的运算逻辑（顺序、分支与循环），因此它与我们常用的命令式语言是等价的(注4)。但是由于存在存储问题，所以命令式语言是时序相关的——即有存取某个存储单元的先后问题。而函数式语言由于“把大象装进冰箱”之后就再也不可更改，因此变得时序无关。
以上述的petri网的例子来讲，由于时序无关，所以图左侧的“库所（圆圈）”中的两个“消息（黑点）”分解成右侧的两个库所来处理时，其转换的代价为0（无锁），而这个过程应用在多核机器或分布式网络上时，效率却提高了一倍。
更深层次地思考这个问题，由于在计算机系统中函数本身仍然是以数据形式存储的，所以函数事实上也是“被运算的对象”和“运算结果”。函数的这种特性被称为高阶函数。“函数等义于值”是函数式的基础，而“函数是值”，则是高阶函数的基础。
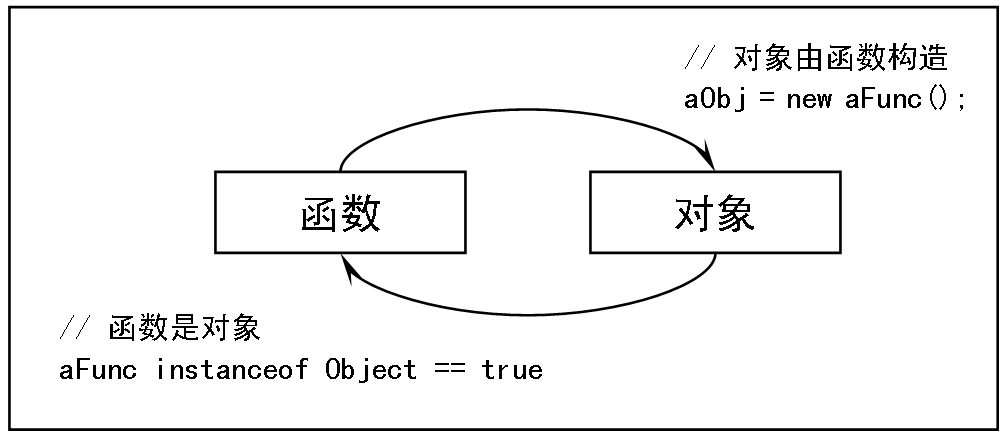图5：JavaScript统一语言范型的基本模型（注5）
当“函数是值”时，我们可以把一个函数传递到另一个地方去运算，而其运算结果仍然是值，所以可以把一个等义的结果再传回来。注意这一过程，就是分布运算的实质，所以，函数式在本质上、天生地就是支持分布运算的。无论我们是将“一段函数式代码”所表达的整个运算过程分解成何种形式，并分布在何种复杂的运算环境或网络环境中，只要最终在逻辑上它能得到一个值序列和一个运算，就能够成为更大范围的分布网络中的一个结点。
而这，就是整个计算世界的全部（注6）：(symbol)。
注1：《Erlang程序设计》中，作者以这个例子为起始，来讲述Erlang变量的单一赋值。
注2：参见《结构程序设计》，讨论“如何刻画计算的进展”时，作者E.W.Dijkstra说：（程序）如果含有循环语句，仅用语法指示器就不能描述计算的进展了……（而应该）引进一个“动态指示器”毫不含糊地累计相应的现行循环的序数……因为，语法指示器无法充当这种坐标系统的一个组成成分。
注3："Implementing Coloured Petri Nets Using a Functional Programming Language" at http://portal.acm.org/citation.cfm?id=993039，and Functional Nets at http://lamp.epfl.ch/fn/
注4：不同范型的计算机语言之间等价问题，可以归结到图灵等价这个命题上，这意味着该运算系统或模型能够执行任何复杂程度的、图灵机可完成的数学运算。2007年，Alex Smith证明了Wolfram提出了最小的“2,3图灵机（两种颜色，三种状态）”模型是最小完备的图灵等价系统。
注5：这个统一过程用到了多项与函数式相关的基本设定：函数是执行体、函数等义于值、函数是值。
注6：与“(+ Xn)”比较，这个表达式认为“运算 +”——也就是某个函数——其实也是值，因此它也是“值系列”Xn中的一个部分。于是，当由自然语义中的symbol来指代Xn时，整个表达式就变成了：(symbol)。建议阅读作者的其它两篇文章：
